Kolmannen asteen yhtälön ratkaisukaava

Kolmannen asteen polynomiyhtälössä y = x³/4 + 3x²/4 − 3x/2 − 2
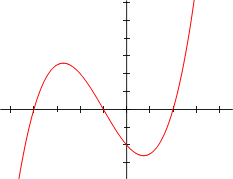
= (1/4)(x + 4)(x + 1)(x − 2) voidaan joskus kirjoittaa tulomuodossa. Tulontekijöistä voidaan päätellä suoraan yhtälön juuret.

Kolmannen asteen yhtälön ratkaisukaava on Niccolò Tartaglian keksimä kaava ratkaista yhtälöt muotoa

$a{x}^3+b{x}^2+cx+d=0,$

missä

$a=0$

. Kun yhtälö jaetaan a:lla ja sijoitetaan x=y-b/3a, saadaan yhtälö muotoon y³+py+q=0. Jos p=0 nähdään, että yhtälöllä on ratkaisuna y=-q^(1/3). Siten y³+py+q=0 on jaollinen polynomilla y-q^(1/3) ja saatu toisen asteen yhtälö on helppo ratkaista. Keskitytään siis tapaukseen, missä

$p=0.$

Sijoittamalla y=u+v yhtälöön y³+py+q=0 saadaan yhtälö muotoon

$u^3+v^3+(3uv+p)(u+v)+q=0.$

Nyt voidaan valita u ja v siten, että 3uv=-p. Tällöin saadaan

$u^3-\frac{p^3}{27u^3}+q=0.$

Tämä näennäisesti kuudennen asteen yhtälö palautuu sijoituksella t=u³ toisen asteen yhtälöksi. Kun nämä arvot on saatu, voidaan päätellä edellisten sijoituksessa saatujen muuttujien arvot ja lopulta polynomin juuret saadaan selville.

Ratkaisut

Suoraan yhtälön kertoimista juuret saadaan kaavoilla: $\begin{array}{cc}{x}_1=& -\frac{b}{3a}\\ & +\sqrt[3]{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})+\sqrt{{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})}^2+{(\frac{c}{3a}-\frac{b^2}{9a^2})}^3}}\\ & +\sqrt[3]{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})-\sqrt{{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})}^2+{(\frac{c}{3a}-\frac{b^2}{9a^2})}^3}}\\ x_2=& -\frac{b}{3a}\\ & +\frac{-1+\sqrt{-3}}{2}\sqrt[3]{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})+\sqrt{{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})}^2+{(\frac{c}{3a}-\frac{b^2}{9a^2})}^3}}\\ & +\frac{-1-\sqrt{-3}}{2}\sqrt[3]{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})-\sqrt{{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})}^2+{(\frac{c}{3a}-\frac{b^2}{9a^2})}^3}}\\ x_3=& -\frac{b}{3a}\\ & +\frac{-1-\sqrt{-3}}{2}\sqrt[3]{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})+\sqrt{{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})}^2+{(\frac{c}{3a}-\frac{b^2}{9a^2})}^3}}\\ & +\frac{-1+\sqrt{-3}}{2}\sqrt[3]{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})-\sqrt{{(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})}^2+{(\frac{c}{3a}-\frac{b^2}{9a^2})}^3}}\\ \end{array}$

Lauseketta

${(\frac{-b^3}{27a^3}+\frac{bc}{6a^2}-\frac{d}{2a})}^2+{(\frac{c}{3a}-\frac{b^2}{9a^2})}^3$

kutsutaan yhtälön diskriminantiksi. Jos kaikki kertoimet a, b, c ja d ovat reaalilukuja ja diskriminantti positiivinen, on yhtälöllä vain yksi reaalinen ratkaisu, josta on edellä käytetty merkintää x₁. Ratkaisut x₂ ja x₃ ovat tällöin kompleksilukuja, jotka ovat toistensa liittolukuja. Mikäli diskriminantti on negatiivinen, on neliöjuuresta saatu luku imaginääriluku. Tällöin molempien ratkaisukaavassa esiintyvien kuutiojuurten sisällä on kompleksiluku, jonka juuren ratkaisemiseksi tarvitaan De Moivren kaavaa. Nämä kuutiojuuret ovat kuitenkin toistensa liittolukuja, minkä vuoksi niiden summa on reaaliluku. Tässä tapauksessa yhtälöllä on siis kolme reaalista ratkaisua (edellyttäen, että kertoimet ovat reaalilukuja).

Aiheesta muualla

• Ohjelma, joka antaa 2., 3. ja 4. asteen yhtälön ratkaisut, kun siihen syötetään kertoimet
• The Cubic Formula