Elementtimenetelmä

Elementtiverkko, jota käytetään magneettikentän mallintamiseen. Eri värit kuvaavat eri materiaaleja: oranssi on käämi, vaaleansininen on ferromagneettinen kappale (esimerkiksi rautaa) ja harmaa on ilmaa.

Elementtimenetelmä (FEM, engl. Finite Element Method) on numeerinen menetelmä differentiaaliyhtälöiden, erityisesti osittaisdifferentiaaliyhtälöiden, ratkaisemiseen tietokoneella. Differentiaaliyhtälöt ovat hyvin yleisiä esimerkiksi fysiikassa, mutta vähänkään monimutkaisemmissa ongelmissa differentiaaliyhtälöä ei voida ratkaista tarkasti niin kutsutussa suljetussa muodossa, eli tavallisten matemaattisten operaatioiden avulla. Niinpä joudutaan tyytymään esimerkiksi elementtimenetelmän antamaan likimääräiseen vastaukseen.

Menetelmä perustuu alkuperäisen jatkuvan ongelman muuntamiseen lineaariseksi yhtälöryhmäksi diskretoimalla, jolloin ongelma voidaan ratkaista tietokoneella. Elementtimenetelmän antama ratkaisu on paloittain polynominen approksimaatio tarkasta ratkaisusta. Helpoimmassa tapauksessa vastaus rajataan ensimmäisen asteen polynomeihin, jolloin ratkaisu on paloittain lineaarinen funktio.

Elementtimenetelmällä saatu ratkaisu yllä olevaan ongelmaan.

Sovellukset

Elementtimenetelmäverkko ihmisen polvinivelestä.

Käytännössä elementtimenetelmää käytetään lähinnä kaksi- ja kolmiulotteisten ongelmien ratkaisuun, sillä yksiulotteisiin ongelmiin on usein helppo löytää ratkaisu analyyttisesti. Menetelmä on hyvin monikäyttöinen, sillä se soveltuu kaikenlaisten osittaisdifferentiaaliyhtälöiden numeeriseen ratkaisemiseen. Elementtimenetelmällä voidaan mallintaa muun muassa rakenteiden taipumista ja niiden kokemia jännityksiä, kappaleen sisäistä sähkönjohtavuutta sekä nesteen tai kaasun käyttäytymistä. Menetelmä luotiin alun perin erityisesti kone- ja rakennustekniikan alalle erilaisten rakenteiden statiikan ja dynamiikan käsittelyyn, mutta nykyään sitä käytetään laajasti eri aloilla, muun muassa lujuusopissa, virtausmekaniikassa, geofysiikassa, sähkötekniikassa, akustiikassa ja bioteknologiassa.

Matemaattinen muotoilu

Yksiulotteinen esimerkki

Tutkitaan esimerkkinä seuraavaa reunaehto-ongelmaa: etsi funktio $u(x)\in C^2(0,1)$, joka toteuttaa seuraavat ehdot:

$\frac{d^{2}u(x)}{d{x}^2}=f(x),x\in [0,1]$

$u(0)=0,u(1)=0$.

Tässä $C^2(0,1)$ tarkoittaa sellaisten funktioiden joukkoa, jotka ovat kahdesti derivoituvia välillä $(0,1)$ ja funktio $f$ tunnetaan.

Heikko muoto

Elementtimenetelmää varten ongelma on kirjoitettava niin sanottuun heikkoon muotoon eli variaatiomuotoon. Tämä tapahtuu kertomalla yhtälö molemmin puolin jollakin reunaehdot täyttävällä funktiolla $v(x)$ ja integroimalla saadun yhtälön molemmat puolet.

$\underset{0}{\overset{1}{\int }}\frac{d^{2}u(x)}{d{x}^2}v(x)dx=\underset{0}{\overset{1}{\int }}v(x)f(x)dx$

Tämän yhtälön vasen puoli voidaan osittaisintegroida, jolloin osittaisintegroinnin toinen termi katoaa sen vuoksi, että $v(0)=v(1)=0$. Saatu ongelma heikossa muodossa on tämän jälkeen

$\underset{0}{\overset{1}{\int }}\frac{du(x)}{dx}\frac{dv(x)}{dx}dx=-\underset{0}{\overset{1}{\int }}v(x)f(x)dx$.

Yllä oleva yhtälö on tarkoitus ratkaista siten, että pyritään löytämään $u$, joka toteuttaa yhtälön kaikilla halutuilla tarpeeksi hyvin käyttäytyvillä funktioilla $v$ (sopiva funktioavaruus $v$:lle on esimerkiksi Sobolevin avaruus). Heikko muoto auttaa ongelman muotoilemisessa lineaarialgebran käsitteiksi. Lisäksi heikon muodon etuna on, että se lieventää hieman ehtoja, joita funktiolta $u$ vaaditaan, jolloin useampi ongelma on ratkaistavissa. Nyt funktion $u$ on oltava vain kerran derivoituva, sen on ratkaistava ongelma vain halutuilla funktioilla $v$ ja lisäksi integraali voidaan määrittää, vaikka $u$ ei olisikaan derivoituva yksittäisissä pisteissä.

Diskretointi

Alkuperäinen funktio (sinisellä) ja sen approksimaatio paloittain lineaarisella funktiolla (punaisella).

Kuvassa on sinisellä kantafunktiot ${\varphi }_k$, joiden lineaarikombinaatio punainen käyrä $w_h$ on.

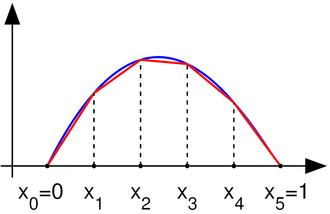
Jotta ongelman voisi ratkaista tietokoneella, vastausta pitää etsiä jostakin äärellisulotteisesta funktioavaruudesta. Elementtimenetelmän tapauksessa vastausta approksimoidaan paloittain määritellyllä polynomilla. Käytetään tässä esimerkissä paloittain lineaarisia funktioita. Lineaariset kantafunktiot ${\varphi }_k$ ovat nyt terävän hatun muotoisia ja ne määritellään seuraavasti:

${\varphi }_k(x)=\{\begin{array}{cc}\frac{x-x_{k-1}}{x_k-x_{k-1}},& \text{ kun }x\in [x_{k-1},x_k],\\ \frac{x_{k+1}-x}{x_{k+1}-x_k},& \text{ kun }x\in [x_k,x_{k+1}],\mathrm{\forall }k=1,\dots ,n\\ 0& \text{ muulloin}\end{array}.$

Otetaan esimerkkiin neljä kantafunktiota. Tällöin mikä tahansa elementtiavaruuteen $V_h$ kuuluva funktio voidaan kirjoittaa tässä kannassa muodossa

$w_h(x)=\sum _{k=1}^4{\alpha }_k{\varphi }_k(x)$

joillain kertoimilla ${\alpha }_k$. Niinpä heikko ongelma elementtiavaruudessa on seuraava: etsi $u_h\in V_h$, jolle pätee

$\underset{0}{\overset{1}{\int }}\frac{d{u}_h(x)}{dx}\frac{d{v}_h(x)}{dx}dx=-\underset{0}{\overset{1}{\int }}{v}_h(x)f(x)dx\mathrm{\forall }{v}_h\in V_h$.

Funktio $u_h$ voidaan kirjoittaa kantafunktioiden avulla muodossa $u_h=\sum _{k=1}^4{\beta }_k{\varphi }_k$. Sijoitetaan tämä yllä olevaan. Nyt ongelmana on löytää kertoimet ${\beta }_k$, joille

$\sum _{k=1}^4{\beta }_k\underset{0}{\overset{1}{\int }}\frac{d{\varphi }_k(x)}{dx}\frac{d{v}_h(x)}{dx}dx=-\underset{0}{\overset{1}{\int }}{v}_h(x)f(x)dx\mathrm{\forall }{v}_h\in V_h$.

Elementtiavaruus $V_h$ on äärellinen ja riittää tarkistaa, että yhtälö toteutuu $v_h$:n ollessa avaruuden kantafunktio. Siispä ongelma voidaan kirjoittaa seuraavasti: löydä kertoimet ${\beta }_k$ siten, että

$\sum _{k=1}^4{\beta }_k\underset{0}{\overset{1}{\int }}\frac{d{\varphi }_k(x)}{dx}\frac{d{\varphi }_i(x)}{dx}dx=-\underset{0}{\overset{1}{\int }}{\varphi }_i(x)f(x)dx$

jokaiselle $i=1,...,4$. Tämän voi nyt kirjoittaa lineaarisena yhtälöryhmänä

$A𝐱=𝐟$,

jossa matriisi $A$ ja vektorit $𝐱$ sekä $𝐟$ on määritelty seuraavasti:

$A_{ik}=\underset{0}{\overset{1}{\int }}\frac{d{\varphi }_k(x)}{dx}\frac{d{\varphi }_i(x)}{dx}dx$

${𝐱}_k={\beta }_k$

${𝐟}_i=-\underset{0}{\overset{1}{\int }}{\varphi }_i(x)f(x)dx$.

Kantafunktiot ja niiden derivaatat sekä funktio $f(x)$ tunnetaan ja matriisin $A$ sekä vektorin $𝐟$ elementit voidaan laskea näistä numeerisesti integroimalla, joten lineaarisesta yhtälöryhmästä voidaan ratkaista vektori $𝐱$. Huomionarvoista on, että matriisi $A$ on symmetrinen, positiividefiniitti ja harva, eli suurin osa sen alkioista on nollia. Saatu lineaarinen yhtälöryhmä on usein niin suuri, ettei sitä kannata ratkaista eksaktisti ja vektori $𝐱$ ratkaistaankin usein esimerkiksi konjugaattigradienttimenetelmällä.

Moniulotteinen esimerkki

Paloittain määritelty lineaarinen funktio kahdessa ulottuvuudessa. Alla näkyy elementtimenetelmässä käytetty verkko ja yllä yksi mahdollinen tätä verkkoa käyttämällä saatu ratkaisu.

Elementtimenetelmä soveltuu hyvin esimerkiksi Poissonin yhtälön ratkaisuun sekä kahdessa että kolmessa ulottuvuudessa. Yhtälö voidaan kirjoittaa Laplacen operaattorilla muodossa:

${\mathrm{\nabla }}^{2}u=f\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{a}\mathrm{\Omega }$

$u=0\text{reunalla}\partial \mathrm{\Omega }$

missä $\mathrm{\Omega }$ on jokin tarpeeksi mukavan muotoinen kaksi- tai kolmiulotteinen alue, esimerkiksi monikulmio. Tämän yhtälön heikko muoto on

$-\underset{\mathrm{\Omega }}{\int }\mathrm{\nabla }u\cdot \mathrm{\nabla }vds=\underset{\mathrm{\Omega }}{\int }fvds$.

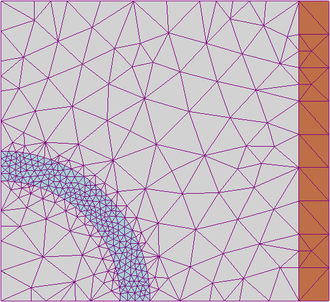
Elementtimenetelmä toimii kaksi- ja kolmiulotteisissa tapauksissa hyvin samalla lailla kuin yksiulotteisessakin. Lineaarinen ongelma muodostetaan heikosta muodosta käytännössä analogisesti yksiulotteisen esimerkin kanssa. Kaksiulotteista ratkaisua varten on muodostettava esimerkiksi kolmioista koostuva verkko, jonka kolmioiden kärkipisteissä aina yksi kantafunktioista on arvoltaan yksi ja kaikki muut nollia. Myös esimerkiksi nelikulmioista koostuvaa verkkoa voidaan käyttää. Lineaarisessa tapauksessa näin muodostuvat kantafunktiot ovat ikään kuin pyramidin muotoisia ja elementtimenetelmän antamat ratkaisut ovat paloittain määriteltyjä lineaarisia funktioita kahdessa ulottuvuudessa. Kolmiulotteisessa tapauksessa verkko taas voi koostua esimerkiksi tetraedreistä.