Kertymäfunktio

Diagrammissa on jatkuvan satunnaismuuttujan kuvaaja, johon on väritetty näkyviin tapahtuman "todennäköisyysmassat". Väritetyn alueen määrätty integraalit eli kuvaajan pinta-alat ovat suhteessa tapahtuman todennäköisyyteen.

Kertymäfunktio eli jakaumafunktio (Malline:K-en, cdf) on todennäköisyyslaskennassa ja tilastotieteessä reaaliarvoisen satunnaismuuttujan todennäköisyyden jakautumista kuvaava funktio. Kertymäfunktion $F(x)$ arvot ovat todennäköisyyksiä tapahtumissa, jossa satunnaismuuttuja $X$ saa reuna-arvon $x$ tai sitä pienempiä arvoja eli $F(x)=P(X\le x)$. Jatkuvan satunnaismuuttujan tapauksessa kertymäfunktio määritellään tiheysfunktion määrätyn integraalin avulla ja diskreetillä satunnaismuuttujalla pistetodennäköisyyksien summana. Kertymäfunktio on aina oikealta jatkuva, vaikka tiheysfunktio tai pistetodennäköisyysfunktio olisi epäjatkuva.

Määritelmä

Diskreetin satunnaismuuttujan kertymäfunktio määritellään

$F(x)=P(X\le x)=\sum _{k\le x}p(k),$

missä $p(k)$ on pistetodennäköisyysfunktion arvo ylärajaa $x$ pienemmillä satunnaismuuttujan arvoilla.

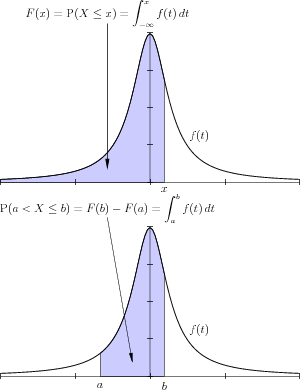
Jatkuvan satunnaismuuttujan kertymäfunktio määritellään määrättynä integraalina ylärajan $x$ suhteen

$F(x)=P(X\le x)=\underset{-\mathrm{\infty }}{\overset{x}{\int }}f(t)dt,$

missä $f(x)$ on satunnaismuuttujan tiheysfunktio. Tiheysfunktiota havainnollistetaan ajattelemalla sen arvoja "todennäköisyysmassan" korkeutena, missä suuri arvo merkitsee yleistä satunnaismuuttujan arvoa. Kertymäfunktion tapauksessa voidaan edelleen ajatella, että sen arvo tarkoittaisi "todennäköisyysmassan" kokonaismäärää $F(a)$ kohdassa $a$ ja sitä pienemmillä satunnaismuuttujan arvoilla.

Jos tiheysfunktio on jatkuva, saadaan se myös derivoimalla kertymäfunktio muuttujan suhteen

$F^{\prime }(x)=f(x).$

Merkintöjä

Jos halutaan korostaa kertymäfunktion satunnaismuuttujaa, merkitään satunnaismuuttuja usein alaindeksiksi $F_X(x)$ ja $F_Y(x).$ Toisinaan merkitään kertymäfunktio kreikkalaisella aakkosella $\mathrm{\Phi }(x)$ (lue: "fii"), jos tiheysfunktio on ollut $\varphi (x)$ (pieni kirjain).

Esimerkkejä

Ylin kuvaaja esittää diskreetin satunnaismuuttujan kertymäfunktiota, keskimmäinen jatkuvan satunnaismuuttujan ja alin sellaisen satunnaismuuttujan, jolla on kumpaakin piirrettä.

Diskreetti satunnaismuuttuja

Diskreetin satunnaismuuttujan pistetodennäköisyysfunktiolla saa 10 nollasta eroavaa arvoa

$P(X=x_i)=p(x_i)=f(x_i),$

kun $i=1,...,10,$ jotka ovat yhtä suuret eli $p(x_i)=\frac{1}{10}.$ Kertymäfunktio saadaan arvoa x pienempien kohtien todennäköisyyksien summasta eli

$F(x)=P(X\le x)=\sum _{x_i\le x}{p}_i=p_1+p_2+...+p_k.$

Tämän porrasfunktion arvot ovat oikealta jatkuvia ja sen kuvaaja on esitetty alla.

Jatkuva satunnaismuuttuja

Tasaisen jakauman tiheysfunktio välillä [a,b] on

$f(x)=\{\begin{array}{cc}\frac{1}{b-a},& \text{jos }x\in [a,b]\\ 0,& \text{jos }x\notin [a,b]\end{array}$

ja sen kertymäfunktioksi saadaan

$F(x)=\underset{-\mathrm{\infty }}{\overset{x}{\int }}f(t)dt=\{\begin{array}{cc}0,& \text{jos }x<a\\ \frac{x-a}{b-a},& \text{jos }x\in [a,b]\\ 1,& \text{jos }x>b.\end{array}$

Sen kuvaaja on alla.

• 
  Diskreetti jakauma, jossa 10 yhtä todennäköistä arvoa
• 
  Binomijakauman kertymäfunktio
• 
  Beta-jakaumia eri parametreilla
• 
  Burrin jakaumia eri parametreillä
• 
  Cauchyn jakaumia eri parametreillä
• 
  Khi-jakaumia
• 
  χ²-jakaumia
• 
  Eksponenttijakaumia kolmella parametrillä
• 
  Frechet-jakaumia eri parametreillä
• 
  Gammajakaumia eri parametreillä
• 
  Maxwell-Boltzmannin jakaumia eri parametreillä
• 
  Normaalijakaumia kuudella parametriparilla
• 
  Pareto-jakamia eriparametreillä
• 
  Rayleigh-jakaumia eri parametreillä
• 
  Tasainen jakauma

Ominaisuuksia

Funktiona

Kertymäfunktio on kuvaus reaaliluvuilta välille $[0,1]$, eli

$F(x):ℝ\to [0,1].$

Jatkuvan satunnaismuuttujan kertymäfunktio on jatkuva funktio. Diskreetin satunnaismuuttujan kertymäfunktio on oikealta jatkuva porrasfunktio. Jatkuvuudesta seuraa ominaisuus

$P(X<a)=\underset{x\to a}{\lim }F(x)=\underset{x\to a}{\lim }P(X<x)=P(X\le a)=F(a).$

Tämä ominaisuus voidaan kirjoittaa havainnollisemmin

$P(X\le a)=P(X<a\text{ tai }X=a)=P(X<a)+P(X=a)=P(X<a).$

Jatkuvan satunnaismuuttujan pistetodennäköisyys eli arvo yksittäisessä pisteessä on siten nolla eli

$P(X=a)=0.$

Koska kertymäfunktion arvot ovat tapahtumien todennäköisyyksiä, saa se vain arvoja väliltä

$0\le F(x)\le 1.$

Kertymäfunktio on lisäksi monotoninen funktio, joka on ei-vähenevä eli

$F(x_1)\le F(x_2)$ kun on $x_1<x_2$.

Tämän vuoksi kertymäfunktio kasvaa lopulta täyteen arvoonsa, kun ylärajaa kasvatetaan riittävästi

$\underset{a\to +\mathrm{\infty }}{\lim }F(a)=\underset{a\to +\mathrm{\infty }}{\lim }\underset{-\mathrm{\infty }}{\overset{a}{\int }}f(x)dx=1.$

Kertymäfunktio alkaa nollasta jostakin arvosta a lähtien. Jos satunnaismuuttuja arvoalue on äärettömän laaja, voidaan tämä ilmaista

$\underset{a\to -\mathrm{\infty }}{\lim }F(a)=\underset{a\to -\mathrm{\infty }}{\lim }\underset{-\mathrm{\infty }}{\overset{a}{\int }}f(x)dx=0.$

Todennäköisyyksinä

Edellä esitelty määritelmä on eräs tapa ilmaista tapahtuma, jossa todennäköisyys lasketaan käyttämällä satunnaismuuttujan ylärajana $x$ eli

$P(X\le x)=F(x).$

Voidaan osoittaa, että sillä voidaan laskea kaikki sellaiset todennäköisyydet, jossa tapahtumat ovat välejä. Esimerkiksi, koska mielivaltaiselle satunnaismuuttujan arvolle $a$ pätee

$P(X<a)+P(a\le X)=1,$

voidaan vastatapahtuman todennäköisyys laskea

$P(a\le X)=1-P(X<a)=1-P(X\le a)=1-F(a).$

Toisaalta, koska mielivaltaisille satunnaismuuttujan arvoille $a$ ja $b$ pätee

$P(X<a)+P(a\le X\le b)=P(X\le b),$

voidaan välin $[a,b]$ todennäköisyys laskea

$P(a\le X\le b)=P(X\le b)-P(X<a)=P(X\le b)-P(X\le a)=F(b)-F(a).$

Jos kertymäfunktio olisi määritelty toisella tavalla, olisi siihenkin voitu johtaa kaikkien muidenkin välien todennäköisyydet.

• 
  $P(X<x)+P(x\le X)=1,$ kohdassa x
• 
  $P(a\le X)=1-F(a)$
• 
  $P(x_1\le X\le x_2)=$ $F(x_2)-F(x_1)$