Moninin–Obuhovin samanlaisuusteoria

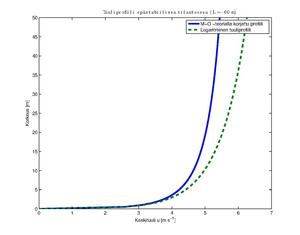
Moninin–Obuhovin teorian ja Businger–Dyerin muotojen ennustama tuuliprofiili, kun tilanne on epästabiili. Vihreä katkoviiva kuvaa korjaamatonta tuuliprofiilia.

Moninin–Obuhovin samanlaisuusteoria kuvaa meteorologiassa tiettyjen rajakerrossuureiden (mm. keskituuli, lämpötila, ominaiskosteus) pystyprofiileja. Se voidaan ajatella laajennuksena logaritmisen tuuliprofiilin ennusteisiin. Siinä missä puhdas logaritminen profiili olettaa ilmakehän olevan neutraali, yrittää Moninin–Obuhovin teoria korjata lukuja sen mukaan, mikä on ilmakehän stabiilisuus. Nimitys "samanlaisuus" viittaa siihen, että teoria esittää rajakerroksen käyttäytyvän kaikkialla samaan tapaan.

Neutraalissa tilanteessa tuulen pystygradientti on muotoa

$\frac{z}{u_{*}}\frac{\partial \overline{u}}{\partial z}=\frac{1}{k}$

missä z on korkeus, $u_{*}$ kitkanopeus ja k von Kármánin vakio (~ 0,4). Ei-neutraalissa tilanteessa Moninin–Obuhovin teoria esittää tätä korjattavaksi universaalifunktiolla ${\mathrm{\Phi }}_m(\zeta )$, jolloin

$\frac{z}{u_{*}}\frac{\partial \overline{u}}{\partial z}=\frac{1}{k}{\mathrm{\Phi }}_m(\zeta )$

Tässä $\zeta =\frac{z}{L}$ on ilmakehän stabiilisuus ja L Obuhov-pituus.

Universaalifunktiolle on olemassa vanhemmat, Joost Busingerin ja Arthur Dyerin tutkimuksiin perustuvat muodot, sekä uudemmat, John Wyngaardin (2010) päivittämät muodot.

Businger–Dyer -muodot

Universaalifunktio on dimensioton. Businger–Dyer -muodot perustuvat Kansasissa tehtyihin mittauksiin ja ovat stabiilille tilanteelle

${\mathrm{\Phi }}_m(\zeta )=1+4.7\zeta$

${\mathrm{\Phi }}_h(\zeta )=0.74+4.7\zeta$

ja epästabiilille tilanteelle

${\mathrm{\Phi }}_m(\zeta )=(1-15\zeta {)}^{-1/4}$

${\mathrm{\Phi }}_h(\zeta )=0.74(1-9\zeta {)}^{-1/2}$

Korjattu tuuliprofiili

Kun Moninin–Obuhovin muodot integroidaan puolittain korkeuden suhteen alkaen niin sanotusta rosoisuusparametrista z₀, saadaan

$\overline{u}=\frac{u_{*}}{k}[\ln \left(\frac{z}{z_0}\right)-{\mathrm{\Psi }}_m(\zeta )+{\mathrm{\Psi }}_m({\zeta }_0)]$

missä on lyhyyden vuoksi merkitty niin sanotut korjausfunktiot ${\mathrm{\Psi }}_m(\zeta )=\underset{0}{\overset{\zeta }{\int }}\frac{1-{\mathrm{\Phi }}_m({\zeta }^{\prime })}{{\zeta }^{\prime }}\text{d}{\zeta }^{\prime }$. Näin ollen esimerkiksi stabiilissa tilanteessa liikemäärän korjausfunktio on ${\mathrm{\Psi }}_m=-4.7\zeta$.

Lämpötilan ja kosteuden profiilit

Lämpötilan ja kosteuden vertikaaliprofiileissa kitkatuulen korvaa skaalalämpötila $T_{*}=-\overline{{{\theta }_v}^{\prime }{w}^{\prime }}/u_{*}$ tai skaalakosteus $q_{*}=-\overline{q^{\prime }{w}^{\prime }}/u_{*}$, sekä tuulen korvaa potentiaalilämpötila tai ominaiskosteus. Tällöin universaalifunktionkin lauseke on erilainen.

$\frac{z}{T_{*}}\frac{\partial \overline{\theta }}{\partial z}=\frac{1}{k}{\mathrm{\Phi }}_h(\zeta )$

$\frac{z}{q_{*}}\frac{\partial \overline{q}}{\partial z}=\frac{1}{k}{\mathrm{\Phi }}_h(\zeta )$

Aiheesta muualla

• American Meteorological Society, Glossary of Meteorology: Monin–Obukhov similarity theory Malline:En
• Universität Bayreuth: Thomas Foken, 50 years of the Monin-Obukhov similarity theory Malline:En (pdf)
• University of Washington: Boundary Layer Meteorology, Lecture 6. Monin-Obukhov similarity theory Malline:En (pdf)