Kirchhoffin piirilait

Kirchhoffin piirilait ovat sähködynamiikan peruslakeja yhdessä Ohmin lain kanssa. Kirchhoffin lakeja on kaksi: Kirchhoffin virtalaki ja Kirchhoffin jännitelaki. Kirchhoffin lait kertovat, miten sähkövarauksen ja energian säilymislakeja voidaan soveltaa virtapiirien suunnitteluun. Kirchhoffin ja Ohmin lakien perusteella voidaan periaatteessa ratkaista jokainen virtapiirejä koskeva tehtävä.

Preussilainen fyysikko Gustav Kirchhoff esitteli virtapiirejä koskevat lauseet vuonna 1845. Hän esitti ensimmäisenä tavan analysoida sähköisiä virtapiirejä käyttäen solmupisteitä ja virtasilmukoita sellaisissa monimutkaisissa tilanteissa, joissa Ohmin laki ei riitä. Kirchhoffin piirilakeja on kaksi: virta- ja jännitelaki. Kummatkin niistä pätevät sekä vaihto- että tasavirtapiireille.

Kirchhoffin virtalaki

Kirchhoffin virtalain mukaan solmupisteeseen tulevien sähkövirtojen summa on yhtä suuri kuin siitä lähtevien virtojen summa: i₁ + i₄ = i₂ + i₃

Kirchhoffin virtalakia kutsutaan myös nimellä Kirchhoffin ensimmäinen laki. Kirchhoffin virtalain mukaan sähkövirtaa ei tule mihinkään pisteeseen enempää kuin sieltä poistuu. Virtapiirin johtimet muodostavat verkon, jonka haarat liittyvät toisiinsa haaroitus- eli solmupisteissä. Näin ollen Kirchhoffin virtalain mukaan sähkövirtaa ei häviä eikä synny johtimien risteyskohdissa.

Täten missä tahansa sähköjohtimien liitoskohdassa toteutuu:

$\mathrm{\Sigma }I=0,$

Eli solmupisteeseen tulevien ja siitä poistuvien virtojen erotus on nolla.

Kirchhoffin jännitelaki

Tiedosto:KVL.png

Kirchhoffin jännitelain mukaan suljetussa virtasilmukassa lähdejännitteiden summa on yhtä suuri kuin jännitehäviöiden summa: v₁ + v₂ + v₃ + v₄ = 0

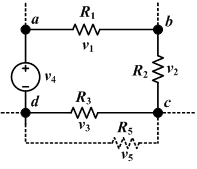
Kirchhoffin jännitelaki tunnetaan myös nimellä Kirchhoffin toinen laki. Jännitelaki perustuu energian säilymislakiin. Sähkövarauksen jännitelähteestä saama potentiaalienergia kuluu sähkövirran kulkuun kaikkien virtapiirin vastusten läpi. Tästä seuraa, että kuljettaessa täysi kierros virtapiirin ympäri potentiaalierojen summan pitää olla nolla.

Kirchhoffin jännitelain mukaan jokaiselle suljetulle silmukalle on toteuduttava:

$\mathrm{\Sigma }V=0.$

Eli suljetussa virtapiirissä lähdejännite on yhtä suuri kuin jännitehäviöiden summa.

Laskentamenetelmä

Kirchhoffin piirilakeihin perustuu laskentamenetelmä, jolla voidaan ratkaista monimutkaisempienkin virtapiirien virtoja sekä myös impedansseja. Menetelmässä hyödynnetään sekä Kirchhoffin virta- että jännitelakia.

• Menetelmän ensimmäisessä vaiheessa merkitään jokaiseen virtapiirin haaraan virta ja sen arvioitu kulkusuunta.
• Lasketaan piirin solmupisteiden lukumäärä n.
• Kirjoitetaan n-1 virtalain mukaista yhtälöä, yhtälöt saa kirjoittaa haluamiinsa virtapiirin solmupisteisiin.
• Loput yhtälöistä kaikkien tuntemattomien ratkaisemiseksi kirjoitetaan jännitelain avulla.

Jänniteyhtälöt saa kirjoittaa mille tahansa reitille, kunhan jokaisen virtapiirin haaran kautta kuljetaan kerran.

Laskuesimerkki

Esimerkissä on esitetty vaihtovirtapiiri, mutta menetelmä pätee myös tasavirtapiireissä.

Tiedosto:E134z1234i1234s12.gifTiedosto:E134z1234s12i1234 electric circuit 3ps 4imp 4cur 2ter.gif

• Lasketaan solmupisteiden lukumäärä n(2).
• Kirjoitetaan n-1 virtalain mukaista yhtälöä.

${\overline{I}}_4={\overline{I}}_1+{\overline{I}}_2+{\overline{I}}_3$

• Kirjoitetaan tarvittava määrä jännitelain mukaisia yhtälöitä (3 silmukkaa, kiertäen myötäpäivään).

${\overline{E}}_1=-{\overline{I}}_1\cdot {\overline{Z}}_1+{\overline{I}}_2\cdot {\overline{Z}}_2$

${\overline{E}}_3=-{\overline{I}}_2\cdot {\overline{Z}}_2+{\overline{I}}_3\cdot {\overline{Z}}_3$

$-{\overline{E}}_3-{\overline{E}}_4=-{\overline{I}}_3\cdot {\overline{Z}}_3-{\overline{I}}_4\cdot {\overline{Z}}_4$

• Nyt voidaan ratkaista virrat ${\overline{I}}_1\Rightarrow {\overline{I}}_4$

Muita virtapiirien laskentamenetelmiä

• Tähtipistepotentiaalimenetelmä
• Nortonin menetelmä
• Theveninin menetelmä
• Silmukkamenetelmä
• Solmumenetelmä

Katso myös

• Tähti-kolmiomuunnos

Kirjallisuutta

• Malline:Kirjaviite
• Malline:Kirjaviite
• Malline:Kirjaviite