Kehäkulma

Kaarta AB (punainen) vastaavat keskuskulma $\alpha =\measuredangle AOB$ ja kehäkulma $\beta =\measuredangle APB$.

Keskus- ja kehäkulma, joka ei muutu sijainnistaan huolimatta.

Kehäkulma on geometriassa ympyrään liittyvä kulma. Ympyrän kehältä valitaan kolme pistettä A, B ja P, joista P:stä piirretään jänteet PA ja PB. Jänteiden PA ja PB välistä kulmaa $\measuredangle APB$ nimitetään kehäkulmaksi. Koska kulman määrittäminen kahden pisteen avulla jättää kaksi vaihtoehtoista tulkintaa, sidotaan keskuskulma usein ympyrän kaareen tai sitä vastaavaan jänteeseen.

Kehäkulmalause

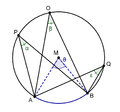
Seuraavaa lausetta kutsutaan kehäkulmalauseeksi: Olkoon $\mathrm{\Gamma }$ annettu ympyrä ja olkoot $A$ ja $B$ kaksi $\mathrm{\Gamma }$:n pistettä siten että $A$ ja $B$ eivät ole $\mathrm{\Gamma }$:n halkaisijan päätepisteet. Jos $C$ ja $D$ ovat samalla puolella suoraa $AB$ olevia $\mathrm{\Gamma }$:n pisteitä, niin $\mathrm{\angle }ACB\cong \mathrm{\angle }ADB$. Tämän tiedon välittömänä seurauksena, mikäli kahdella kehäkulmalla $\measuredangle A{P}_{1}B$ ja $\measuredangle A{P}_{2}B$ on yhteinen keskuskulma $\measuredangle AOB$, ovat kehäkulmat suuruudeltaan puolet tästä ja siten yhtäsuuret eli $\measuredangle A{P}_{1}B=\measuredangle A{P}_{2}B=\beta$. Kaikki saman kaaren kehäkulmat ovat siksi aina yhtä suuria, kuten alla olevassa kuvassa näytetään.

• 
  Samalle keskuskulmalle kuuluvat kehäkulmat ovat aina saman suuruiset: α = β = ε.
• 
  Kaksi pistettä jakavat kehän kahteen kaareen, joihin kehäkulmalausetta voidaan erikseen soveltaa.

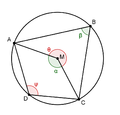
Kehäkulmalauseella on yksinkertaisuudestaan huolimatta merkittävä asema euklidisessa geometriassa, jossa sen ominaisuuksia käytetetään paljon todistamisessa. Esimerkiksi, kun kaksi ympyrän jännettä leikkaavat toisensa, voidaan kehäkulmalauseella osoittaa, että jänteiden osien tulo on vakio. Myös tunnettu tulos, jossa jännenelikulmion vastakkaisten kulmien summa on 180°, saadaan kehäkulmalauseella pääteltyä helposti.

Kehäpisteen ollessa kaaren päätepisteessä, voidaan käsitellä tilannetta poikkeavasti, koska kehäkulma näkyy nyt jänteen ja tangentin välissä.

Viimeinen huomautus nähdään yllä olevasta kuvasta. Kaarta ADC vastaavat keskuskulma α ja kehäkulma β. Kaarta CBA vastaavat keskuskulma θ ja kehäkulma ψ. Koska θ = 360° − α, ovat kehäkulma puolet tästä eli ψ = 1/2·θ = 1/2·(360° − α) = 180° − α/2 = 180° − β. Täten vastakkaiset kulmat ovat suplementtikulmat eli ψ = 180° − β.

Kun kehäpiste lähestyy kaaren reunapistettä, jää toisen kehäkulman jänne lyhyeksi. Kehäkulman suuruus säilyy saman suuruisena lähestymisen loppuun saakka, mutta kun kehäpiste yhtyy kaaren reunapisteeseen, näkyy kehäkulman aukeama sen toisen kylkenä olevan jänteen ja ympyrän tangentin välissä. Tätä erikoistilannetta voi pitää kehäkulmalauseen laajennuksena (katso viereinen kuva).

Thaleen lause

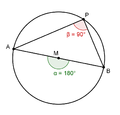
Kehäkulmalauseen erikoistapauksena saadaan Thaleen lause, kun keskuskulma on oikokulma eli 180°, niin kehäkulma on suora kulma eli 90°. Kehäkulmalauseen mukaisesti kaksi (eli kaikki) puoliympyrän kehäkulmaa ovat molemmat suoria.

• 
  Oikokulman takana oleva kehäkulma on suora kulma kummalla puolella halkaisijaa tahansa.
• 
  Kaikilla kehäpisteillä on puoliympyrässä sama kulma $\measuredangle ABC=90^{\circ }$

Kehäkulmalauseen todistus

Lause on ollut tapana todistaa Suomen koululaitoksen oppikirjoissa yhdessä erikoistapauksessa ja kahdessa yleisessä tapauksessa, jotka kattavat kaikki tapaukset ja tukevat toisiaan todistelussa.

Kehäkulman jänne ja sektorin säde ovat päällekkäin

Apukuvio todistukseen erikoistapauksessa, jossa kehäkulman kylki ja sektorin kylki ovat päällekkäin.

Tutkimalla kuviota huomataan, että

• kehäkulma on $\measuredangle BVA$ ja keskuskulma on $\measuredangle BOA$.
• janat VO = OB = OA = R eli ympyrän säde.
• tasakylkisessä kolmiossa $\mathrm{△}VOA$ kärki O on huipun kärki ja A ja V ovat kantakulmien kärjet.
• kantakulmat $\measuredangle OVA$ = $\measuredangle VAO$ = $\psi$ ja huippukulma on keskuskulman vieruskulma $\measuredangle AOV=180^{\circ }-\measuredangle BOA=180^{\circ }-\theta$

Kolmion $\mathrm{△}VAO$ kulmien summa on $\psi +\psi +180^{\circ }-\theta =180^{\circ }\iff \theta =2\psi$, aivan kuten kehäkulmalause väittääkin. Tähän tulokseen vedotaan kahdessa alemmassa osassa.

Keskuskulma mahtuu kokonaan kehäkulman sisälle

Apukuvio todistukseen erikoistapauksessa, jossa keskuskulma mahtuu kehäkulman sisälle.

Piirretään kehäpisteestä V keskipisteen O kautta kulkeva halkaisija kehäpisteeseen E. Jana VE jakaa kaaren DC osiin DE ja EC. Huomataan, että

• kaarta EC vastaavat keskuskulma $\measuredangle EOC$ ja kehäkulma $\measuredangle EVC$. Tilanne on sama kuin todistuksen ensimmäisessä osassa, jolloin kehäkulman jänne ja sektorin säde olivat päällekkäin. Sen perusteella ${\theta }_2=2{\psi }_2$.
• kaarta DE vastaavat keskuskulma $\measuredangle DOE$ ja kehäkulma $\measuredangle DVE$. Silloin, kun vedotaan taas todistuksen ensimmäiseen osaan, on ${\theta }_1=2{\psi }_1$.
• Kehäkulmaksi $\measuredangle DVC$ saadaan ${\psi }_0={\psi }_1+{\psi }_1$.

Keskuskulma $\measuredangle DOC={\theta }_0={\theta }_1+{\theta }_2=2{\psi }_1+2{\psi }_2=2({\psi }_1+{\psi }_2)=2{\psi }_0,$ aivan kuten kehäkulmalause väittääkin.

Keskuskulma mahtuu vain osittain kehäkulman sisälle

Apukuvio todistukseen erikoistapauksessa, jossa keskuskulma mahtuu vain osittain kehäkulman sisälle.

Piirretään kehäpisteestä V keskipisteen O kautta kulkeva halkaisija kehäpisteeseen E. Jana VE osuu kaaren DC viereen muodostaen kaaret ED ja EC. Huomataan, että

• kaarta EC vastaavat keskuskulma $\measuredangle EOC$ ja kehäkulma $\measuredangle EVC$. Silloin, kun vedotaan uudestaan todistuksen ensimmäiseen osaan, on ${\theta }_0=2{\psi }_0$.
• kaarta ED vastaavat keskuskulma $\measuredangle EOD$ ja kehäkulma $\measuredangle EVD$. Silloin todistuksen ensimmäisen osan mukaisesti on ${\theta }_1=2{\psi }_1$.
• Kehäkulmaksi $\measuredangle DVC$ saadaan ${\psi }_2={\psi }_0-{\psi }_1$.

Keskuskulma $\measuredangle DOC={\theta }_2={\theta }_0-{\theta }_1=2{\psi }_0-2{\psi }_1=2({\psi }_0-{\psi }_1)=2{\psi }_2,$ aivan kuten kehäkulmalause väittääkin.

Historia

Eukleideen (noin 300 eaa.) kirjassa Alkeet käsitellään kehäkulmia 3. kirjassa väittämien 20, 21 ja 22 muodossa. Väittämät olivat "kehäkulma on puolet keskuskulmasta" , "samaa kaarta vastaavat kehäkulmat ovat saman suuruiset" ja "vastakkaisten kaarien kehäkulmien summa on 180°" .

Thales (636–546 eaa.) esitti oman lauseensa paljon aikaisemmin, mutta se oli kehäkulmalauseen erikoistapaus. Hän on kuitenkin oppinut sen kauppamatkoillaan Babyloniassa. Tämänkin lauseen Eukleides liitti Alkeisiin 3. kirjaan väittämäksi 33.